4 Marzo 2010By Richard
Saggezza ET: Geometria, Vibrazione e Dimensioni Superiori
– 13.1 Il collegamento tra dimensioni, geometria e vibrazione
Ora dovremmo essere più che pronti per una piena rivelazione sul significato e l’importanza della geometria dei Solidi Platonici nel comprendere le proprietà multidimensionali delle “unità di coscienza”, come abbiamo visto sulla Terra.
Per ricordare, il nostro termine “unità di coscienza” (CU) si riferisce ad un’area dove l’”etere”, energetico e conscio, detto anche energia di punto zero, passa nella nostro spazio e tempo fisico, prendendo la forma di una sfera luminosa di energia elettromagnetica con un foro nel mezzo, che forma un asse di rotazione nord-sud.
Dagli ultimi due capitoli, ora sappiamo che queste formazioni di energia sferiche mostrano vortici geometrici in esse. Questa formazione viene da investigazioni scientifiche sui comportamenti planetari e da analisi matematica degli angoli “tetraedrici” e dei rapporti tra i vari oggetti localizzati nell’area di Cydonia su Marte, che sembrano creati artificialmente.
Formazioni allineate come queste solitamente si pensano come prodotte dall’uomo e non parte della natura e quindi per molti di noi l’informazione in questo capitolo sarà unica. Non abbiamo mai cercato di insinuare che i pianeti abbiano cristalli giganti fisici in essi, ma solo che questa sarebbe la forma presa dall’energia nel fluire attraverso la CU, che a sua volta forma il pianeta. Non siamo abituati a pensare al suono e al colore come aventi forme geometriche nella propria vibrazione, ma questo è esattamente quello che la nostra ricerca ci ha portato a concludere.
– 13.1.1 Vortici Interdimensionali
Negli ultimi due capitoli abbiamo visto come tutti i pianeti mostrino segni del possedere flussi energetici in certi punti geometrici, definiti da forme come l’icosaedro, il dodecaedro e il tetraedro. Fussi energetici in entrata e uscita dai poli, con quelli che sembrano due campi controrotanti che si uniscono per formare questi schemi geometrici sulla superficie del pianeta. (Discuteremo del come e del perchè di questa azione congiunta negli ultimi capitoli). Molto probabilmente esiste, nel nucleo, materiale luminoso simile a quello nel Sole, all’interno dei pianeti e i problemi col modello della dinamo richiedono una migliore soluzione.
Tornando alla nostra discussione delle aree geometriche, sulla Terra abbiamo visto che queste aree possono anche avere un effetto potente sullo stato “vibrazionale” della materia fisica e sulle condizioni dello spazio e del tempo. In breve, sembra che:
Queste aree dei nodi geometrici sono in qualche modo vortici di energia “interdimensionali”
Abbiamo già ipotizzato che questo avvenga perchè le “dimensioni superiori” sono semplici aree attorno a noi, dove l’energia eterica vibra a frequenza superiore rispetto al nostro livello. Ora che abbiamo visto la geometria del tetraedro, dell’icosaedro e le altre nell’intero Sistema Solare, dovremmo aspettarci che tutti i pianeti stiano creando questi vortici gravitazionali e interdimensionali dello spazio e del tempo allo stesso modo. Cosa interessante, nella serie della Legge dell’Uno dal presunto gruppo extraterrestre conosciuto come Ra nel 1981, viene fornita informazione specifica sulla comprensione della vibrazione come “collegamento mancante” per capire le dimensioni superiori.
A loro non piace usare la parola “dimensioni” ma le chiamano “densità”, indicando che sarebbero diverse densità dell’Unica Fonte di Energia Eterica di cui abbiamo scritto in questo libro. La prima citazione riguarda le densità nelle vibrazioni del suono e la seconda riguarda le vibrazioni del colore:
RA: Il termine densità è, come lo definite, matematico. L’analogia più vicina è quella della musica, dove dopo sette note nella vostra scala occidentale, la nota numero otto inizia una nuova ottava.
RA: La natura della vibrazione è tale che può essere vista come avente scalini vicini. Questi scalini possono essere visti come aventi dei confini. In ogni confine ci sono sfumature infinite di vibrazione o colore.
Comunque, avvicinandosi al confine, serve uno sforzo per superarlo. Questi colori sono un modo semplificato per esprimere le divisioni della vostra densità. (B2, 42)
Nelle prossime citazioni da RA possiamo vedere che sono consapevoli delle energie geometriche che abbiamo osservato sul pianeta, restiamo quindi nell’idea delle dimensioni superiori connesse alla vibrazione di un fluido:
RA: Immaginate i molti campi di forza della Terra nella loro rete geometricamente precisa. Le energie fluiscono nei piani della Terra, come li chiamereste, da punti determinati magneticamente. (B1, 81-82)
RA: L’amore che crea luce, divenendo amore/luce, fluisce nella sfera planetaria secondo la rete di punti elettromagnetici o di entrata. Questi flussi sono quindi disponibili all’individuo che, come il pianeta, è una rete di campi di energia elettromagnetica con punti di entrata. (B1, 144)
Citazioni dal libro Seth Speaks di Jane Roberts, dalle sessioni condotte nel 1986, parlano chiaramente dei vertici degli oggetti geometrici come “punti di flusso” interdimensionali e vanno oltre nel dettaglio:
…Altri tipi di coscienza coesistono nello stesso “spazio” che il vostro mondo abita…Voi non li percepite e parlando genericamente loro non vi percepiscono. Questa è una affermazione generica, comunque, vari punti della vostra realtà coincidono, per dire. Questi punti non sono riconosciuti come tali, ma sono punti di quella che potreste chiamare doppia realtà, contenendo grande potenziale energetico; punti coordinati in cui le realtà si mescolano. Esistono punti principali, matematici, fonti di fantastica energia e punti subordinati, in gran numero.
(Nota: questi punti “matematicamente puri” a cui si riferisce Seth, sono i vertici delle geometrie Platoniche di cui abbiamo discusso. Il mescolarsi delle realtà viene osservato nel Triangolo delle Bermuda. Seth potrebbe anche parlare del fatto che due campi differenti si mescolino in questi punti per creare le loro qualità di vortici, quindi l’uso della parola “doppi”)
(Lunga pausa a 9:29) Esistono quattro punti di coordinata assoluti che intersecano tutte le realtà.
(Nota: L’unico Solido Platonico che ha quattro punti è il tetraedro. La citazione di Seth qua suggerisce che il tetraedro è in qualche modo “più importante” delle altre geometrie, come anche Hoagland crede dal Messaggio di Cydonia e più avanti vedremo il motivo.)
Questi punti di coordinata (geometrica) agiscono anche (in generale) come canali attraverso i quali fluisce l’energia e come percorsi invisibili o pieghe tra una realtà e l’altra. Agiscono anche come trasformatori e forniscono molta dell’energia generativa che crea continuamente nei vostri termini. (Molte pause).
(Nota: Come ha mostrato il lavoro di Richard. C.Hoagland e di “The Enterprise Mission”, i punti del tetraedro sono in effetti la fonte di flussi di grande energia nei pianeti, come la Grande Macchia Rossa di Giove. Ancora, i punti dell’icosaedro sulla Terra mostrano chiaramente passaggi tra una realtà e l’altra. Come regola generale, quando troviamo molte pause nelle parole di Jane che canalizza Seth, significa che si trova in trance profonda per portare l’informazione.)
Il vostro spazio è pieno di questi punti subordinati e come vedrete più avanti, questi sono importanti perchè voi possiate trasformare i pensieri e le emozioni in materia fisica. Quando un pensiero o una emozione guadagna una certa intensità, automaticamente attrae il potere di uno di questi punti subordinati che viene caricato e in un certo senso ingrandito, ma non di dimensione.
Questi punti si trovano in quello che chiamate tempo e spazio. Ci sono certi punti nel tempo e nello spazio, (sempre nei vostri termini) che conducono più di altri, in cui idee e materia saranno più carichi. In pratica, questo significa che le costruzioni dureranno più a lungo; nel vostro contesto queste idee sposate alla forma saranno relativamente eterne. Le piramidi, per esempio, sono appropriate al punto.
(Nota: Questo può confondere ora, ma poi vedremo come queste geometrie influiscano sul tempo come suggerisce Seth. La citazione di Seth sulla materia più forte in questi punti combacia con le nostre osservazioni per cui la materia è molto più flessibile di quanto pensavamo. In diverse circostanze come nei tornado, la materia può cambiare fase e divenire più debole e ora Seth ci dice che le stesse forze, in forma meno caotica, possono anche rinforzarla.)
(Lento al 9:43) Queste coordinate, assolute, principali o subordinate) rappresentano accumuli o tracce di pura energia, punti estremamente piccoli se pensate alla dimensione, molto più piccoli di ogni particella conosciuta ai vostri scienziati per esempio, ma composti di pura energia. Questa energia deve venire attivata. Resta dormiente fino a quel momento e non si può attivare fisicamente.
(Nota: Questo è quello che troveremo esattamente all’inizio della della Parte Due, a livello subatomico, la geometria è la chiave nascosta all’”energia pura” dell’etere)
(9:50) Ora: Alcuni indizi che possono aiutare voi o i matematici. Esiste una minuta alterazione delle forze di gravità nelle vicinanze di questi punti, anche dei subordinati e tutte le cosiddette leggi della fisica ad un estremo o l’altro, avranno un effetto ondulatorio in queste vicinanze. I punti subordinati servono anche come supporti, come intensificazione strutturale nella fabbrica dell’energia che forma le realtà e le manifestazioni. Mentre sono tracce o accumuli di pura energia, c’è grande differenza tra la quantità di energia disponibile nei vari punti subordinati e tra i punti principali e assoluti..(sessione 524)
(Nota: Questa predizione si manifesta nell’osservazione del Vortice dell’Oregon, ovviamente una di tali aree di carica energetica. La gravità si modifica notevolmente in questo vortice, così come il passaggio del tempo e le dimensioni degli oggetti fisici.)
Quindi, nelle aree come quelle dei dodici vortici dell’icosaedro sulla Terra di Sanderson, l’informazione derivata da extraterrestri ci dice che questi effetti bizzarri ci mostrano casi in cui l’etere simil-fluido vibrante passa nella nostra realtà con una densità maggiore rispetto all’energia normalmente attorno a noi. Se questa energia è di maggior “densità”, allora trasformerebbe tutta la materia nelle sue vicinanze, inclusa la vita umana, portandola a densità maggiore. Qua abbiamo una nuova spiegazione per i fenomeni in cui abbiamo investigato.
L’idea di Ra delle “dimensioni superiori” come parte di una Ottava di densità da un valido senso e una risposta a molti dei correnti paradossi scientifici.
Dobbiamo quindi vedere che esiste un singolo “etere” nell’universo e segue il comportamento della musica e della vibrazione per differenziarsi. Questo spiega completamente molti misteri, mentre esploriamo il prossimo capitolo. Seth chiarisce questo punto:
Ora qualunque cosa appaia in termini fisici esiste anche in altri termini che non percepite. Percepite le realtà solo quando raggiungono un certo “tono”, quando sembrano divenire materia. Esistono però piuttosto validamente anche ad altri livelli.. (sessione 530)
(Nota: Notate l’uso della parola “tono”, non è una semplice metafora, ma un’affermazione accurata dell’Universo Armonico e del suo funzionamento con densità di energia eterica.)
Il vostro non è un sistema di realtà formato dalla concentrazione di energia più intensa. E’ semplicemente quello in cui siete sintonizzati, di cui siete parte. Lo percepite solo per questa ragione. Altre porzioni di voi stessi quindi, di cui non siete consapevoli, abitano quello che chiamereste un supersistema di realtà in cui la coscienza apprende come gestire e percepire concentrazioni maggiori di energia e a costruire “forme” di natura differente.. (sessione 530)
Altra citazione:
Voi capite che esistono spettri della luce. Quindi esistono spettri della materia. Il vostro sistema di realtà fisica non è densa rispetto ad altri. Le (tre) dimensioni che date alla materia fisica iniziano appena a suggerire le varietà di dimensioni (che sono) possibili..
(sessione 567)
Ancora, abbiamo l’analogia degli “spettri” di dimensioni, in altre parole, che esistono in una struttura ad Ottava. La stessa materia, formata di etere, deve essere soggetta ai cambiamenti dei suoi livelli vibrazionali e quindi potenzialmente in grado di muoversi da una realtà ad un’altra.
Questo potrebbe spiegare come i tornado possano fondere assieme oggetti solidi e perchè avvengano sparizioni nei vortici icosaedrici sulla Terra. Inoltre, Seth e Ra insistono dicendo che la nostra coscienza è il legame chiave che ci connette con questi altri livelli di realtà; siamo, infatti, esseri multidimensionali che hanno perso la consapevolezze del “grande disegno”.
Tenendo questo in mente, a questo punto diviene utile una investigazione nelle proprietà della luce, del suono e delle vibrazioni geometriche e in come lavorino assieme. Sarà materiale generico, ma è vitale prima di procedere nel prossimo capitolo di discussione sulle dimensioni. Sia Seth che Ra suggeriscono che è necessario esplorare queste proprietà interconnesse della vibrazione per trovare le risposte più profonde.
– 13.2 Suono
Il modo più semplice e famigliare per studiare la vibrazione è attraverso il suono. Ogni musicista vi dirà che tutte le vibrazioni del suono sono raggruppate in ottave e sappiamo che “ott” indica il numero otto. In una ottava ci sono sette “nodi” fondamentali di vibrazione seguiti da un ottavo. L’ottava nota ha due propositi, non completa solo una ottava ma inizia la seguente.
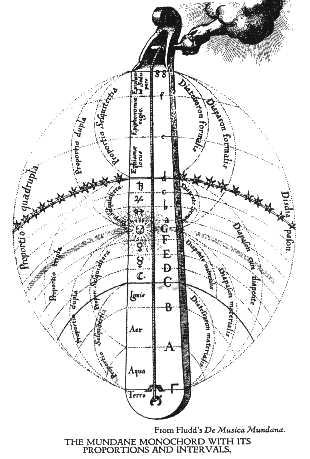
Il matematico greco e filosofo Pitagora, attraverso un processo di divisione ripetuta della frequenza per cinque, è riconosciuto per aver mostrato questi otto toni “puri” dell’ottava, conosciuta come scala Diatonica. Ha iniziato con uno strumento “monocorda” e ha misurato le lunghezze quando venivano suonate diverse note.
Quindi, come con la chitarra, ha premuto il dito in diversi punti della corda e ha suonato diverse note. Ogni nota ha diviso la corda in diverse sezioni, quindi ha misurato le lunghezze delle due sezioni e le ha accoppiate ad ogni nota.
Pitagora ha quindi mostrato che la frequenza (o velocità di vibrazione) di ogni nota può essere rappresentata come rapporto tra le due lunghezze della corda o due numeri, da qui il termine “rapporto Diatonico”. Ulteriori ricerche con divisione per cinque lo hanno portato a costruire l’Ottava come raggruppamento più semplice dei vari rapporti coinvolti, come 1:1, 2:1, 3:2, 5:3, 13:8 e 21:13.
Possiamo vedere la scala Diatonica su un piano nei tasti bianchi, la nota iniziale nella nostra ottava è Do. Il piano ha anche i tasti neri e quando li includiamo, abbiamo in totale tredici note nell’Ottava, con la tredicesima che è anche la prima dell’ottava seguente.
Queste tredici note sono conosciute come scala Cromatica e molta della musica mondiale consisterà solo di note che rientrano in questa scala; quindi quasi tutte le canzoni possibili sono eseguibili al piano. (Con una eccezione, la musica Indiana userà note che non rientrano nella scala cromatica, chiamate quartitoni o microtoni).
Matematica a parte, la ragione principale per la scelta del numero otto invece che del tredici per il raggruppamento ad “ottave” di noste musicali, è che tutte le note “diatoniche” suoneranno bene assieme; in altre parole saranno armoniche.
Potete suonare una canzone sui tasti bianchi del piano e sembrerà sempre musica, non importa quale nota suonate. Se sperimentate con la scala cromatica senza conoscere quello che fate, seguirà una dissonanza dolorosa e chiunque nella stanza vi chiederà di fermarvi.
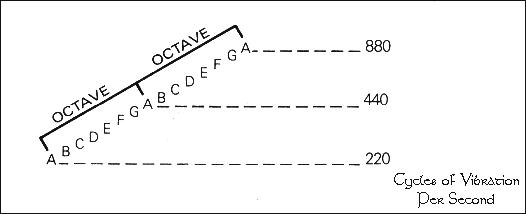
Matematicamente, la nota più alta in una Ottava ha una velocità di vibrazione o frequenza doppia rispetto alla nota più bassa e questo è il modo più basilare per vedere come una Ottava organizzi un gruppo intero di vibrazioni sonore.
Ogni nota, che sia La, Si, Do, Re, Mi, Fa o Sol, avrà un valore doppio nell’ottava seguente.
Dato che le ottave raddoppiano continuamente in vibrazione, esiste un pugno di ottave nel limite percepibile dall’uomo. Oltre un certo punto le vibrazioni saranno troppo veloci per la sensibilità dell’orecchio umano anche se esisteranno ancora attorno a noi.
– 13.2.1 Tutte le vibrazioni possibili
Come l’alfabeto fornisce tutte le parole possibili nel nostro linguaggio, la struttura ad ottava fornisce tutte le possibili variazioni del suono e rivela il modo più semplice in cui si raggruppano. La teoria del caos chiamerebbe l’Ottava un “attrattore”, perchè tutte le vibrazioni sonore, per quanto “caotiche” o casuali possano essere da una all’altra, devono essere “attratte” in una struttura ad Ottava.
Cosa diciamo dei suoni non-musicali come quello del vento chiederete? Come potrebbe il suono del vento rientrare in una Ottava di note musicali? “Rumore Bianco” è il termine tecnico per alta-velocità, fluttuazioni casuali di frequenze sonore che non producono un tono apparente, ma creano un rumore fischiante.
Benchè possano esserci migliaia di frequenze sovrapposte in questo rumore, sappiamo che quando vengono isolate propriamente, ognuna deve essere parte di una Ottava. Semplicemente sono troppi toni diversi prodotti troppo rapidamente perchè le nostre orecchie possano separarli.
– 13.2.2 Il suono è semplicemente la vibrazione dell’aria
Da un punto di vista scientifico, un suono è definito come vibrazione delle molecole dell’aria. Matematicamente, misuriamo i suoni in termini di vibrazioni dell’aria in un secondo di tempo. Questo ci fornisce un valore numerico e quindi chiunque abbia suonato uno strumento a corda sa che il diapason medio dirà “Do 440”
Significa che la nota che chiamiamo LA viene riconosciuta come 440 vibrazioni dell’aria in un secondo di tempo. Una nota diversa avrebbe un numero diverso e quindi 440 vibrazioni dell’aria per secondo devono sempre essere La. Tutto qua. Più avanti vedremo che questi valori “armonici” sono di importanza tremenda nel misurare e analizzare il comportamente dell’etere.
Frequenze numeriche della Scala Diatonica:
288:RE
324:MI
360:FA
384:SOL
432:LA
480:SI
540:DO
576:RE
(Nota: “La” leggermente corretta, spieghiamo più avanti)
Premettendo che non siete in un vacuum totale, la densità o composizione dell’aria che vibra non importa, in quanto uno strumento musicale suonerà ugualmente in cima al Monte Everest, dove l’aria è più sottile, che al livello del mare dove l’aria è più densa.
Persino l’aria stessa non è necessaria, tutto quello che serve è qualcosa che vibri. Per esempio, possiamo sentire questi stessi suoni sott’acqua, come con le canzoni delle balene. Il metallo di un diapason può creare fermando la sua base al vostro cranio e lasciandolo risuonare attraverso il vostro corpo. Quindi il medium non influenza direttamente il tono del suono; le vibrazioni possono avvenire in aria pulita, aria sporca, acqua pulita, acqua sporca, metallo, carne, ossa o altre forme, anche nelle fibre dei vestiti, come nel caso del vecchio “telefono” fatto di due lattine legate da una corda.
In questo caso, quando la stringa viene tirata tra le due lattine e una persona parla nella sua lattina mentre l’altra ascolta, la corda trasporterà le vibrazioni sonore allo stesso modo, anche se saranno distorte. In breve, le vibrazioni del suono non avvengono solo nell’aria, vibrano fondamentalmente attraverso tutto. Sentire il suono è un modo per noi di percepire e sperimentare le vibrazioni.
Benchè siamo abituati a pensare a queste vibrazioni sonore come significative solo per le nostre orecchie, questo libro è iniziato mostrandoci che queste semplici vibrazioni dell’Ottava sottostanno a tutta la realtà che conosciamo. Il “fluido incompressibile” dell’etere invisibile o “energia spirituale” che forma l’Essere Definitivo del nostro universo, può essere mostrato nel vibrare secondo questi principi, come abbiamo visto sui pianeti.
Quindi, come gli Hindu hanno proposto l’idea del AUM come suono primario che ha formato la Creazione, ora possiamo vedere che il suono costruisce l’Universo e la musica è un modo per noi di sentire fisicamente e sperimentare l’essenza di Dio. Noi siamo composti di forme d’onda musicali viventi e danzanti; la creazione di Dio. Senza musica nelle nostre vite, ci neghiamo la conoscenza e la gioia della nostra esistenza.
– 13.3 Luce
Un identico livello di questa ottava di vibrazione avviene nello spettro della luce visibile, dove abbiamo la luce bianca che può essere divisa in un arcobaleno di sette colori, rosso, arancione, giallo, verde, blu, indaco e viola, prima che inizi una ottava di vibrazioni superiore, come l’infrarosso e l’ultravioletto. Ora sappiamo che la frequenze della luce visibile, come “disturbo” ondulatorio di energia eterica similfluido, è semplicemente su una ottava di vibrazione superiore delle frequenze del suono nell’ottava musicale.
Per dirla semplicemente, potete prendere i rapporti numerici tra ogni nota nella scala Diatonica musicale e raddoppiarli molte volte e troverete gli stessi rapporti tra le velocità vibrazionali nello spettro della luce. L’unica differenza tra essi è la magnitudine; il suono vibra molto più lentamente, mentre la luce vibra molto più rapidamente.
Da Fisica dell’Amore di Dale Pond: “Le relazioni di sopra sono derivate dal calcolo delle frequenze e degli intervalli Pitagoreani iniziando nella gamma audio del suono (ndt: soundme.com/theory/teoria6.htm).
Benchè ci siano molte tonalità di Verde che vanno da sopra SI a sotto RE, c’è solo un LA a 512cps nell’ottava audio inferiore. Questi colori riguardano i pigmenti e non le sfumature della luce che sarebbero DO=Rosso, RE=Arancione, MI=Giallo, FA=Verde, SOL=Blu, LA=Indaco e SI=Viola
– 13.3.1 Velocità della Luce
Quando le frequenze della luce o le lunghezze d’onda viaggiano attraverso lo spazio, si muovono a quella che molti credono essere velocità costante, citata come circa 186.000 miglia per secondo. Questa osservazione però non tiene conto della conduzione della luce in un medium eterico ad una data velocità.
Molti pensano che nulla nell’universo possa superare questa frequenza, quindi la velocità della luce o “c” è il movimento più rapido o vibrazione che normalmente riconosciamo dalla nostra prospettiva qua sulla Terra nella terza dimensione. Nuove fonti suggeriscono che “c” sia solo la vibrazione più rapida in condizioni naturali nella terza dimensione.
Come pubblicato nel The New York Times del 2000, condizioni anormali in laboratorio, come in un tubo con gas al cesio sotto grande pressione e illuminato dalla luce “lateralmente”, possono portare la luce a viaggiare 300 volte più velocemente di “c”. Questo risultato è identico a quello degli esperimenti di “interferometria con onde scalari” di Bearden.
Quindi se raggruppassimo tutte le possibili vibrazioni in un grafico, avremmo totale assenza di movimento in fondo al grafico e la velocità della luce in cima. In questo modo la velocità della luce definisce il limite delle vibrazioni nella nostra realtà.
Diversamente da quanto suggerito da Einstein, spostando un oggetto alla velocità della luce può non creare infinita densità nella materia; fonti come Ra categorizzerebbero la velocità della luce come il picco di vibrazioni in terza densità o dimensione.
Se ci muoviamo in un’area o “dominio” in cui l’etere si muove a velocità maggiore, allora la velocità della luce cambia e la materia si “sintonizza” in questo nuovo livello vibrazionale. Questo si conforma con le osservazioni delle anomalie nei tornado e nei vortici, come modifiche nello spazio, nel tempo e nella materia.
Le prime parole nel libro della Genesi nella Bibbia sono, “All’inizio Dio disse, “E luce sia” e ci fu la luce”. Infine possiamo dimostrare che tutte le vibrazioni che creano il nostro universo sono semplicemente forme diverse di questa unica energia conscia.
Senza vestire e vedere i brillanti rossi, blu, verdi, gialli, porpora e arancioni della Luce attorno a noi ci neghiamo la vera conoscenza interiore e la gioia della nostra esistenza. Una vita senza colore è infatti “grigia” e “debole”, “triste” e “nera”.
– 13.4 Geometria
La geometria completa la triade di base della nostra percezione dei mattoni fondamentali della vibrazione nell’Universo, la triade come luce, suono e geometria. Con le geometrie di cui abbiamo discusso, i suoni della musica e i colori dell’arcobaleno prendono forma. Improvvisamente i concetti astratti dell’armonia e del colore rivelano strutture composte di linee dritte e curve con cui possiamo fare modelli e costruire cose. Benchè possiamo vedere colori e sentire suoni, normalmente non pensiamo alla forma geometrica in due o tre dimensioni, come rappresentazione di queste vibrazioni.
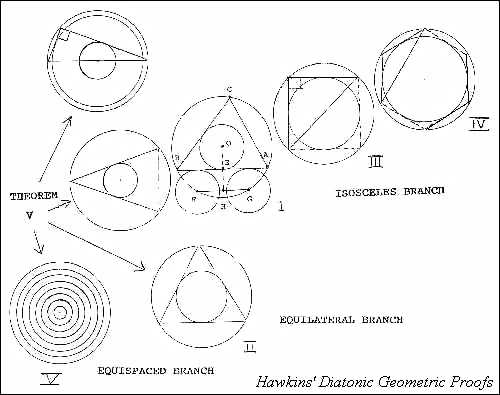
Numerosi ricercatori come Gerald Hawkins, Buckminster Fuller e Hans Jenny hanno mostrato che le vibrazioni del suono formeranno specifici schemi geometrici, se quello che fate vibrare sarà visibile invece dell’aria, normalmente invisibile. Gerald Hawkins non è arrivato alle sue scoperte studiando la vibrazione. Nel suo caso ha fatto le sue scoperte studiando per anni il fenomeno dei “cerchi nel grano”, in cui complesse forme geometriche appaiono di notte in vari campi nel mondo, solitamente visibili solo dall’alto.
Dopo aver studiato centinaia di formazioni, Hawkins ha realizzato che certi schemi si ripetevano e l’unità sottostante a questi schemi era espressa usando forme geometriche bidimensionali come il triangolo, il quadrato e l’esagono e mettendole in un cerchio in modo che i vertici toccassero la circonferenza.
Con sua sorpresa, l’area delle geometrie interne, quando divise per l’area dei cerchi esterni, mostrava la stessa relazione responsabile per le vibrazioni della musica nell’Ottava, i “rapporti diatonici” di cui abbiamo discusso. Questo è esattamente ciò che ha dimostrato Pitagora con il suo strumento “monocorda”, solo che ora invece del rapporto delle lunghezze della corda, abbiamo il rapporto della geometria che indica la stessa cosa.
Ha realizzato che questo era un nuovo set di teoremi in geometria e nessuna autorità accademica che consultò li conosceva. Quindi in due dimensioni, possiamo capire il suono come una vibrazione geometrica “piatta”, come il triangolo, che emerge in un cerchio “piatto”.
13.4.1 Il Pallone di Fuller
Benchè il lavoro di Hawkins apparisse nel 1980 e riguardasse solo due dimensioni, esperimenti seguenti di studiosi del Dr.Buckminster Fuller furono i primi a provare che le vibrazioni del suono sono tridimensionali nella loro struttura. Gli studenti di Fuller hanno usato un pallone sferico bianco per ottenere questo effetto, immergendolo in una tinta di colore scuro e facendola vibrare con frequenze sonore Diatoniche.
Come atteso, la tinta ha potuto raccogliersi e rimanere in quelle aree del pallone con minor movimento. Queste aree erano distanziate da “nodi” o punti in cui tutti i movimenti violenti sulla superficie del pallone si annullavano in una “zona nulla” dove la tinta poteva accumularsi facilmente. Inoltre, deboli e dritte linee di tinta connettevano questi nodi. In questo modo, il suono diviene direttamente visibile come forme geometriche tridimensionali lungo le linee dritte sul pallone.
Guardando queste forme, ricordiamo che rientrano perfettamente in una sfera e che i loro vertici sono i “nodi” rilevati inizialmente. E’ anche importante ricordare che la sfera è la forma più armonica di tutte, creando la base per tutte le altre geometrie in essa.
13.4.2 Cimatica
Il Dr.Hans Jenny è rimasto colpito dalle scoperte di Fuller e dei suoi studenti, per cui le vibrazioni sono tridimensionali e ha cercato di provarlo in modi più semplici che l’uso del pallone nella tinta. Nello studio scientifico del Dr.Jenny conosciuto come “Cimatica”, ha mostrato la geometria delle vibrazioni sonore usando un contenitore pieno di sabbia, Lygodium, intonaco e varie forme di liquido con particelle fini ma visibili o “colloidi” in esso. Gli esperimenti con liquido colloidale sono molto utili per noi.
A riposo, i colloidi sarebbero distribuiti per il liquido, che apparirebbe acqua sporca. Il Dr.Jenny si riferisce a questo stato come “dispersione idrodinamica”. Quando il contenitore veniva vibrato con toni diatonici puri, le particelle nel liquido si raccoglievano in schemi geometrici visibili e ordinati, molti dei quali possono essere visti di struttura sia bidimensionale che tridimensionale.
In altre parole, si possono guardare le immagini che si formano e percepirne chiaramente la profondità, non erano semplicemente “piatte”. Questa è una delle cose più importanti da studiare e ricordare, perchè fornisce una prova visiva irrifiutabile dei concetti di cui abbiamo discusso.

Come descritto prima, esistono solo cinque forme tridimensionali da considerare e le conosciamo come Solidi Platonici.
E’ importante chiarire che guardando queste forme stiamo guardando la vibrazione. Le forme stesse non “esistono” come oggetto fisico, come un ologramma, se cercaste di prenderle o disturbare, esse sparirebbero. Quando non disturbate, le forme hanno esistenza come vibrazione e questa esistenza può creare pressione, come la spinta che sentite sul corpo da un forte suono o da quello di un tuono.
Ora che abbiamo visto queste vibrazioni che operano in un etere simil-fluido, sappiamo che le loro linee di forza che inducono pressione ci forniscono una nuova visione delle dinamiche della gravità. Con la visione delle caratteristiche strutturali della superficie della Terra, come continenti, creste sottomarine e picchi di montagna, modellate da queste geometrie, non ci può essere ancora nascosta la verità. E’ solo questione di tempo prima che questa semplice osservazione divenga conoscenza comune per l’umanità.
E’ importante menzionare che quando gli studenti di Fuller hanno incrementato la frequenza nel pallone o Jenny ha incrementato la frequenza nell’acqua, le vecchie forme si dissolvevano e sparivano e venivano sostituite da forme geometriche più complesse. Questo può funzionare anche al contrario, quando la frequenza viene decrementata al punto originale, riemergono le geometrie precedenti in modo esatto.
Quindi, studiando le dinamiche dell’etere vedremo che quando incrementate la frequenza vibrazionale (o stress) dell’energia nell’area locale, la geometria stessa in quell’area, come quella che da forma alla Terra, si trasformerà spontaneamente in un ordine di complessità superiore. Questo innalzamento e abbassamento di frequenza avviene in tutta la Creazione, inclusi i corpi nel nostro sistema solare che si muove nella Galassia.
Il laovor del Dr.Spilhaus ci ha mostrato che il nostro campo gravitazionale sulla Terra è già passato in diverse trasformazioni dal tempo del “megacontinente” Pangea, che rappresenta il tempo in cui la Terra aveva una crosta uniforme, prima del movimento di allargamento che vediamo ora nella scienza della Tettonica ad Espansione Globale, nata nel 1933 con Otto Hilgenberg.
– 13.5 Spirali
I semplici schemi geometrici formati dalle vibrazioni del suono (quindi anche dalle vibrazioni della luce su una magnitudine superiore) possono essere visti in 2 e 3 dimensioni e le forme bidimensionali come il triangolo, il quadrato e l’esagono discusse da Hawkins, probabilmente ci sono più famigliari che le forme tridimensionali rivelate da Fuller e Jenny, benchè ora le abbiamo viste in azione sui pianeti. Cosa molto importante, queste geometrie vibrazionali possono anche crescere e contrarsi e semplici strutture geometriche visibili organizzano e controllano questi movimenti. Quando iniziamo ad incastrare queste forme una nell’altra, appaiono “incastonate”, con ogni forma successiva che cresce armonicamente rispetto a quella precedente.
Mostreremo altro più avanti. Questa geometria della “sfera nella sfera” è stata osservata in vari esperimenti e ora possiamo attenderci l’esistenza di varie armonie geometriche in queste sfere che si espandono. Il modo più semplice per modellare l’espansione geometrica da una forma all’altra è tracciando il modo in cui i nodi si muovono relativamente tra loro. Ricordiamo che sulla Terra, i movimenti di espansione geometrica sono stati chiamati “radiali” o “a spirale” da Spilhaus e altri.
Il modo più semplice per mappare il movimento da nodo a nodo tra due forme diverse sarebbe con una linea a spirale, che Ra chiama “la linea a spirale della luce”. Queste spirali includono quella di Fibonacci o Rapporto Aureo e spirali create dalla radice quadrata di due, tre e cinque. Ora mostreremo che queste spirali sono direttamente collegate alle frequenze musicali tramite la matematica.
– 13.5.1 La Spirale Phi
Fondamentale per tutti gli studi delle spirali è la più importante, conosciuta come spirale di Fibonacci, del Rapporto Aureo o “phi”. Per comprendere meglio questa spirale, iniziamo con il modo più armonico e vibrazionale attraverso la somma numerica. Essenzialmente, vedremo che ogni nuovo numero è la somma dei due precedenti. Tipicamente iniziamo con uno e lo sommiamo a sè stesso. Questo ci da risultato di due. Quindi prendiamo due e lo sommiamo al numero precedente, che era uno e abbiamo tre. Quindi prendiamo tre e lo sommiamo al precedente, che era due e abbiamo cinque. Continuando abbiamo: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
Quindi i numeri continuano ad espandersi in un modo semplice e armonico, in cui ogni numero rappresenta la somma dei due numeri che venivano prima. Se dividiamo le coppie di numeri sopra riportati tra loro, nei primi stadi vedremo tutti i rapporti Diatonici comuni che Pitagora ha scoperto, come 3/2, 5/3, 8/5, 13/8 e 21/13. Questo non dovrebbe sorprenderci dato che la musica è un movimento vibrazionale e la tecnica di somma usata nel phi è una forma di vibrazione. La natura elegante di questa vibrazione si vede facilmente nei disegni della “spirale phi”, visibile sotto. Per comprendere meglio come questa spirale agisca nei Solidi Platonici, andrebbe vista come oggetto tridimensionale, avvolta attorno ad un cono con il vertice superiore su G e l’inferiore su A. Questo tipo di forma tridimensionale a spirale è chiamata “elica conica”.
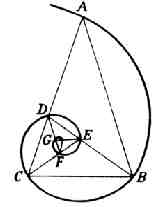
Benchè gli stadi iniziali della serie numerica “phi” formerà i rapporti musicali tra i numeri, col salire delle coppie numeriche, i rapporti tra essi diverranno sempre più simili e il processo di crescita si stabilizza. Infine, salendo ogni coppia di numeri nella serie si dividerà per formare lo stesso numero, ovvero il rapporto tra tutti i numeri rimane costante.
Per questa ragione, il rapporto è chiamato “costante” in quanto sarà sempre lo stesso e il numero (che continua all’infinito) è: 1.618033988749894848820..
Altro fatto interessante è che noi possiamo iniziare con qualsiasi coppia di numeri, non importa la differenza e iniziare a sommarli usando la forma suddetta. Non importa quanto possano essere differenti, in breve creeremo ancora il rapporto costante “phi”. Questo concetto ha ispirato generazioni di matematici, musicisti, scienziati e filosofi, in quanto si rivela in molti modi diversi, inclusa la proporzione di crescita delle piante, degli esseri umani e degli animali. Come abbiamo detto, il rapporto musicale di “phi” fornisce la struttura per la semplice geometria in due e tre dimensioni, che sappiamo essere altra forma di vibrazione. Il diagramma di sopra lo dimostra, possiamo dire che ci sono sei triangoli isosceli di proporzioni identiche rappresentati con l’espansione della spirale. Il rapporto dimensionale tra ogni triangolo sarà la costante “phi” di 1.618… suddetta.
Queste spirali possono mostrarci come semplici forme geometriche come il quadrato e il triangolo possano crescere o ridursi. Con l’espandersi o il contrarsi della spirale, così faranno le forme geometriche che possono esservi formate all’interno. (In altre parole, se la spirale di sopra si aprisse all’esterno, allora i triangoli diverrebbero progressivamente più grandi. Se la spirale si comprimesse all’interno verso il punto F, così i triangoli diverrebbero sempre più piccoli.)
E’ questo principio della spirale che permette ai semplici schemi di espansione della Natura di formularsi, sia nelle strutture cristalline che negli organismi viventi. Se disegnassimo la geometria dell’espansione delle forme geometriche sul pallone di Fuller con l’innalzarsi della vibrazione, vedremmo che le loro espansioni potrebbero essere mappate con le semplici e armoniche spirali suddette.
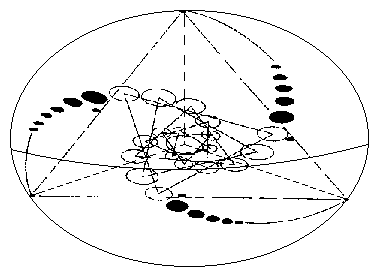
Il diagramma di sopra deriva da una enorme formazione nei campi chiamata “Julia Set triplo” che è apparsa di notte in un campo di grano in Inghilterra nel 1996. E’ un modello di come questo sistema di spirali interconnesse e geometria Platonica appare quando espanso in tre dimensioni.
La formazione originale consisteva solo delle tre spirali fatte da cerchi individuali e le linee dritte, la sfera esterna e l’equatore sono aggiunte per illustrare meglio quello che vediamo. Infine, è un modello per la vibrazione dell’etere che crea gli stress energetici planetari visibili e strutture misurabili nel tempo. Per ora dovremmo visualizzare ogni triangolo come un tetraedro con il suo campo sferico, che rende questo un diagramma geometrico di sfere di energia posizionate come una “mastrioshka” di bambole che abbiamo visto in molti esperimenti come quelli del Dr.Chernobrov.
– 13.6 Forma e Crescita, Spazio e Tempo, Maschio e Femmina
Possiamo vedere perchè gli Antichi si riferivano alle linee dritte e curve come ai due opposti nell’Universo, benchè siano unificate come vibrazione. Infine sentiamo che in un certo modo di pensare, le linee dritte e le geometrie possono rappresentare lo spazio e le linee curve e le spirali possono rappresentare il tempo. Per ora useremo termini più famigliari e diremo che le linee dritte creano la forma e le linee curve creano il movimento e la crescita di questa forma. In altre parole, le linee dritte formano le strutture geometriche delle vibrazioni e le linee curve formano i percorsi di queste frequenze strutturate perchè si espandano e contraggano.
Benchè normalmente non pensiamo alla geometria curva nel suono e nella luce, sappiamo che queste spirali governano il movimento tra una nota nell’ottava e la nota superiore seguente o tra un colore nello spettro e il colore seguente. Per mettere questo in un contesto spirituale, in molte antiche tradizioni mistiche la linea dritta era la forza masculina, associata col Sole e la linea curva era la forza femminina associata con la Luna. Queste associazioni mascolino-femminino sono facili da elaborare intuitivamente nella nostra mente.
A riposo, la cellula di sperma forma una linea dritta, mentre l’ovulo è di forma rotonda. I corpi degli uomini sono più duri e dalle linee dritte rispetto ai corpi delle donne che sono più morbidi e rotondi come lineamenti. Le menti maschili tendono a pensare in modo più lineare, rigido e matematico, col “cervello sinistro” e le menti delle donne tendono a pensare in modo più fluido, emotivo, con gli schemi del “cervello destro”.
L’uomo primitivo cacciava e costruiva con la luce del Sole, usando strumenti dritti come frecce per cacciare, ora invece con tavole dritte, martelli e chiodi per costruire, mentre le donne cucinavano e servivano il cibo con strumenti rotondi come ciotole e nutrivano i loro piccoli con i seni rotondi nell’oscurità di caverne, igloo, tende, lontane dalla luce del giorno a causa dei predatori. Inoltre, le donne sono connesse direttamente con la Luna in modi in cui non sono gli uomini, tramite il loro ciclo mestruale, mostrando altro livello per cui gli Antichi associavano lo spirito femminino col nostro Sole di Mezzanotte.
– 13.7 Geometria sacra e Vita
Lo studio di queste varie forme geometriche e spirali, incluse le connessioni spirituali con l’umanità come parzialmente illustrato sopra, è conosciuto come “geometria sacra” e il libro di Robert Lawlor con lo stesso titolo è forse il riferimento migliore esistente sul soggetto.
Molti dei grandi studiosi di storia hanno approfondito i principi della geometria sacra, in quanto affascinati nello scoprire che le forme di vita di ogni varietà sulla Terra hanno dimostrato che questi principi musicali e vibrazionali coinvolgono lo spazio e il tempo, con linee dritte e curve. I semplici gusci danno una rappresentazione perfetta della spirale di Fibonacci, così come la crescita delle piante, le impronte digitali, il corno di un bue, il girasole o il loto e molte diverse proporzioni nelle strutture scheletriche degli animali e degli esseri umani. Non ci sono limiti nell’estensione della presenza di questi principi, se qualcuno volesse studiare matematicamente ogni pianta o organismo.
Dato che i nostri scienziati non ci danno ragioni per credere che tali principi armonici siano necessari nella crescita delle forme di vita, allora perchè esistono? Se queste proporzioni non fossero importanti allora perchè le vediamo con questa ripetitività? Stiamo semplicemente ignorando l’evidenza attorno a noi, che prova che tutto nell’Universo è prodotto dalla vibrazione? Se l’energia fondamentale che crea la realtà vibra in risonanza armonica, è possibile che qualcosa non abbia una base armonica?
– 13.8 Rapporti di spirale nei solidi platonici
Possiamo dimostrare che le spirali connettono tutti i Solidi Platonici assieme e mostreremo un estratto da The Shift of the Ages. Nel libro di Robert Lawlor Sacred Geometry, apprendiamo che gli Hindu risolsero le geometrie dei Solidi Platonici in una struttura ad ottava come vediamo per il suono e la luce e nella prossima tavola abbiamo elencato questa geometria in ordine.
Questo ci da una visione unificata di come le varie vibrazioni lavorino assieme, cosa che vedremo nel prossimo capitolo. Per ora, dovremmo sapere cosa rappresenta questo grafico. Questo è formato assegnando una lunghezza “l” ai bordi del cubo e quindi confrontando con esso la grandezza dei bordi di altre forme. Ricordiamo che nei Solidi Platonici, ogni faccia ha la stessa forma, ogni angolo è identico, ogni linea ha la stessa lunghezza.
1. Sfera (senza apici)
2. Icosaedro Centrale 1/phi^2
3. Ottaedro 1/sq.rt.2
4. Tetraedro a Stella sq.rt.2
5. Cubo 1
6. Dodecaedro 1/phi
7. Icosaedro phi
8. Sfera (senza apici)
Proporzioni armoniche dei Solidi Platonici
Nel prossimo capitolo descriveremo come gli Hindu conoscessero tutto quello di cui abbiamo discusso su questi campi energetici e oltre. Siamo stati fortunati e abbiamo trovato una rara ristampa del libro di Rama Prasad del 1894, Nature’s Finer Forces: The Science of Breath and the Philosophy of the Tattvas, della Kessinger Publishing. Vedremo che la parola “tattvas” ha un significato simile alla nostra parola “vibrazione”.
La quantità di sovrapposizione tra quello che abbiamo visto fino ad ora e i dati nel libro di Prasad è impressionante, come molto dell’aspetto chiave del modello eterico di cui abbiamo parlato è contenuto nelle pagine di questo libro in una forma o un’altra.
Guarderemo anche da vicino come il concetto antico eterico di una “ottava” di dimensioni si relazioni con gli studi scientifici moderni e mostri che serva poco per rettificare le due opinioni assieme. Inoltre, comprendendo come la geometria si intersechi con le dimensioni superiori, come abbiamo visto nei pianeti, l’idea di una “fisica iperdimensionale” esce dal reame della speculazione nell’arena della scienza applicata. Applicando questi concetti, apriamo la porta verso l’Universo.
Traduzione a cura di Richard
divinecosmos.comDavid Wilcock