di Michele Vassallo da Altrogiornale
Cos’è l’accelerazione di Coriolis? E’ un fenomeno fisico che si verifica in un oggetto che si muove di moto rettilineo su una superficie rotante.
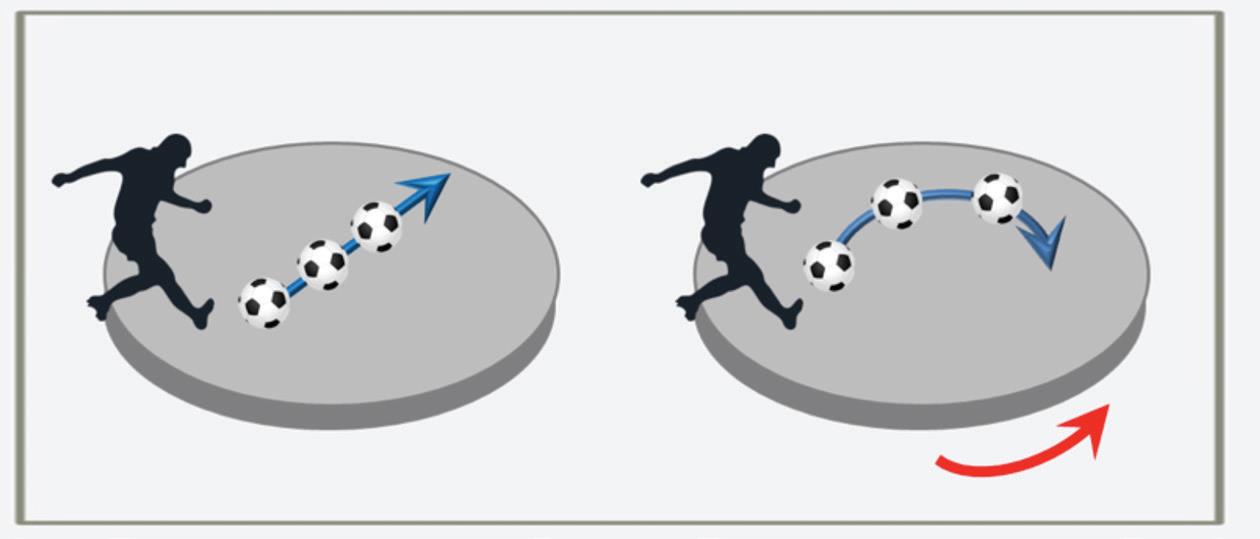
Diamo uno sguardo alle immagini sopra: nella prima foto la palla si sta spostando in linea retta su una piattaforma stazionaria. La palla non è influenzata da alcuna accelerazione laterale perchè la piattaforma è immobile. Quando la piattaforma inizia a ruotare, la palla inizia a piegare la sua traiettoria e il risultato sarà un movimento non più rettilineo. Questa accelerazione laterale, che porta la palla a curvare, è nota come accelerazione di Coriolis. È un fenomeno particolare che può essere utilizzato per dimostrare che la Terra non ruota attorno al proprio asse.
Per fare un esempio, consideriamo che la palla cominci il suo movimento esattamente al centro della piattaforma circolare. La piattaforma ruota, diciamo, alla velocità di 0,1 giri al secondo, ovvero 6 giri al minuto cioè 0,628 rad/sec (1 giro al minuto vale circa 0,1 radianti al secondo e dovresti ricordare che 2π radianti sono 360 °).
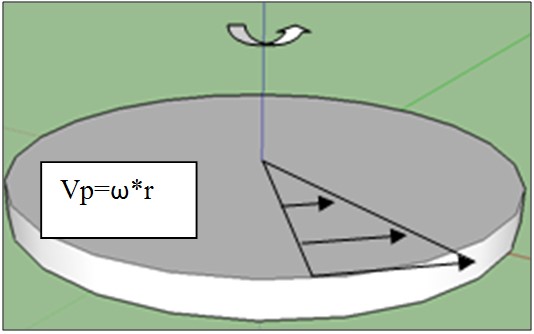
La palla è inizialmente al centro della piattaforma, quindi non viene trascinata da nessuna parte a causa della velocità periferica della piattaforma. Al centro infatti la velocità periferica è, a tutti gli effetti, zero e aumenta spostandosi verso la periferia proporzionalmente al raggio, secondo alla relazione lineare:Vp=ω∙r
dove Vp è la velocità periferica, ω è la velocità angolare, r è il raggio che descrive la posizione della palla sulla piattaforma; r può variare da zero al centro a R che è il raggio esterno.
Quindi, quando la palla inizia il suo movimento rettilineo dal centro alla periferia della piattaforma, risente, nel suo movimento, della velocità periferica di rotazione, che aumenta costantemente, a causa dell’aumento del raggio.
La palla dovrebbe iniziare ad avere un’accelerazione laterale nel senso di rotazione, al fine di mantenere il suo movimento rettilineo.
Tuttavia questo non è possibile, a meno che non riceva una spinta dall’esterno. Quindi, inizia a rimanere indietro lateralmente a causa dell’inerzia, e la traiettoria si piega come mostrato nell’immagine ad inizio articolo.
L’accelerazione laterale che la palla dovrebbe assumere, per mantenere la sua traiettoria lineare, deve essere espressa con la seguente formula:Ac=2∙V∙ω
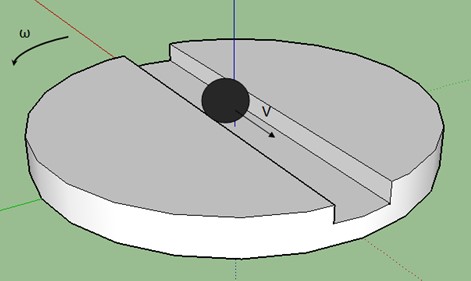
dove Ac si chiama accelerazione di Coriolis, V è la velocità della palla in direzione radiale e ω è la velocità angolare della piattaforma. In questo esempio, la palla è libera di muoversi in qualsiasi direzione. Così, quando la piattaforma inizia la sua rotazione, la palla rimane indietro come conseguenza delle leggi di inerzia. Ma ora, considera il caso in cui la palla viene guidata lateralmente sulla piattaforma, come puoi vedere nella figura che segue. La palla è costretta a seguire la piattaforma e muoversi in modo rettilineo verso il bordo. La palla, in questo modo, ruota con la stessa velocità di rotazione ω della piattaforma.
Per mantenere questo movimento rettilineo della palla sulla piattaforma, la guida deve imprimere sulla palla la forza di Coriolis:Fc=m∙a=m∙2∙V∙ω
dove m è la massa della palla. Questa è una vera forza, non apparente. La forza di Coriolis è apparente per un sistema di riferimento fisso, ma è una forza reale se consideriamo un sistema di riferimento che ruota con la piattaforma.
Applichiamo ora questa idea alla Terra e, più specificamente, agli aeroplani che sorvolano la Terra.
Un aereo, muovendosi su una direzione puramente est-ovest, non sarà influenzato dall’effetto Coriolis, perché la velocità del globo sulla latitudine fissa non varia.
Ma un aereo, decollando da A (vedi la figura), non arriverà al punto A’ (direzione nord-sud come mostrato in figura), a meno che la sua traiettoria non venga riadattata con l’ausilio di un’accelerazione di Coriolis adeguata, ma raggiungerà il punto X.
Facendo qualche ricerca navigando in rete, si può scoprire che gli aeroplani hanno un sistema elettronico in grado di correggere la traiettoria in modo adeguato. Ma è vero?
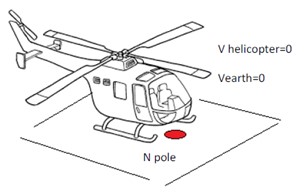
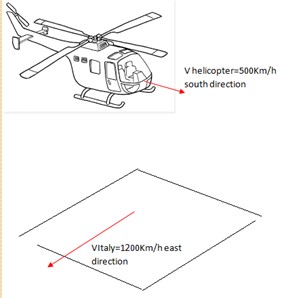
Indaghiamo. Considera ora un elicottero in grado di volare ad una velocità massima di 500 Km/h e che decolla dal Polo Nord.
La Terra trascina l’elicottero, finchè esso non è in volo, con la sua velocità periferica, perché il polo è sull’asse, r = 0, quindi Vp = 0 dove Vp è la velocità periferica. Supponiamo che l’elicottero decolli e voli in direzione esclusivamente sud e che la sua velocità abbia una sola componente meridionale di 500 Km/h. Vediamo cosa succede sotto l’elicottero.
Mentre continua a volare verso sud, la Terra sottostante continua ad accelerare a causa della sua rotazione in direzione est-ovest come effetto dell’aumento del raggio, perché r aumenta. Quando l’aereo arriva all’equatore, r = R cioè 6371 Km, dovrebbe mantenere una velocità periferica di circa 1700 Km /h. La velocità periferica del globo infatti aumenta man mano che ci si allontana dal polo. L’aereo può correggere la sua traiettoria? No perché anche se inizia a seguire la terra lungo l’equatore, può raggiungere solo 500 Km/h. Il carburante è finito, l’aereo tenta di atterrare ma viene distrutto nello stesso istante del suo atterraggio.
Per il lettore medio questa situazione potrebbe sembrare troppo teorica. Quindi diamo un esempio tratto dalla vita di tutti i giorni. Immagina un uomo sdraiato sul suo letto e pronto a alzarsi. Immagina un tapis roulant che si muove sotto il letto all’altezza dei suoi piedi ad una sorprendente velocità di 1000 km/h. Potrebbe l’uomo essere in grado di alzarsi e iniziare subito le sue attività? Assolutamente no. Sarebbe, senza dubbio, sbattuto lontano dal suo letto e schiacciato da qualche parte contro il muro.
Questa è una chiara dimostrazione del fatto che la terra non si muove attorno al suo asse. Se la Terra fosse un globo i paralleli ruoterebbero a velocità differenti a seconda del loro raggio misurato a partire dall’asse di rotazione terrestre. Un corpo libero che si alza dalla Terra, mantiene la velocità di trascinamento del parallelo da cui si è sollevato. Portandosi su un differente parallelo, avente velocità periferica diversa, si dovrebbe vedere la Terra che inizia a muoversi sotto di esso, ma questo non accade.
Questa è una prova del fatto che la Terra non ruota attorno al proprio asse. Un calcolo più preciso verrà fatto nel prossimo articolo.
Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Tra le sue migliori scoperte c’è la reintroduzione dell’etere nella fisica della terra piatta e una nuova visione della natura della luce.
E’ coautore del libro “The real measures of the (flat)Earth” edito da Aracne editore e del blog “rifugiatidipella.com“. Dal 2019 produce materiale video inerente la Terra piatta sul suo canale Youtube “earthmeasured”.