di Michele Vassallo su Altrogiornale
Così come abbiamo fatto con il sole andiamo a calcolare i numeri che ci consentono di descrivere il cono della luna. Useremo le formule già usate per il sole e che abbiamo cercato di generalizzare nell’articolo “Una formula per la traiettoria del sole“.
Abbiamo capito ormai, con l’articolo “Il moto della luna sulla Terra piatta” che la traiettoria della luna è una spirale conica che si sviluppa tra i due tropici.
La luna ha un numero d’ordine n = 9; ricordiamo che il sole è n = 6. Il numero 9 in effetti sembra descrivere bene la luna, così come il 6 descrive bene il sole. Si pensi al ciclo siderale di 27,32 giorni (9 × 3 più frattali) o alla librazione in latitudine della durata di 18,5 anni (9 × 2 più frattali). La figura che segue mostra che, nell’antico sistema geocentrico, la luna era considerata in nona posizione: la più vicina alla Terra.
Il sole 6 e la luna 9 ci richiamano alla mente lo Ying e lo Yang. Il falso allunaggio è stato orchestrato nel 1969. I numeri di questi avvenimenti, lo sappiamo, non sono mai scelti a caso.
La prima costante const1 per la luna sarà:
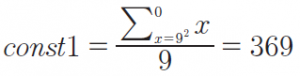
La seconda costante sarà:
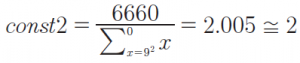
Dobbiamo approssimare il valore della seconda costante in modo da poter fare una descrizione frattale. Non ci interessa infatti la precisione dei decimali ma la natura frattale della realtà. Avendo determinato n = 9, const1 = 369, const2 = 2 possiamo scrivere tutti i dati del cono della luna come riportati nella tabella seguente:
| Raggio [km] | Altezza [km] | |
| Orbita piccola | 9 x 369 x 2 = 6642 | 9 x 369 x 2 = 6642 |
| Orbita grande | 9 x 369 x 4 = 13284 | 9 x 369 x 1 = 3321 |
Poiché il cono della luna non passa esattamente sui tropici, chiamerò le due orbite esterne orbita più piccola (quella vicino al Tropico del Cancro) e più grande (quella inferiore ma più grande vicino al Tropico Capricorno).
Possiamo immediatamente vedere che il cono della luna è molto vicino al cono del sole, solo un po’ più in basso. È chiaro che questa è una descrizione approssimativa: descriviamo solo il frattale più grande. Sappiamo infatti che il cono della luna non è sempre lo stesso e oscilla da -5 ° a + 5 ° attorno al cono del sole, intersecandolo ogni 18,5 anni.
Come abbiamo visto nell’articolo passato questo cono viene percorso in modo spiraliforme dalla luna in modo molto più veloce rispetto al sole. Sappiamo infatti che, mentre il sole impiega un anno per percorrere il suo cono su e giù, la luna ci impiega appena 27,32 giorni. La luna risulta però essere più lenta del sole nel percorrere un singolo giro della spirale. La luna infatti percorre un giro sulla Terra in 24 ore 50 minuti, perdendo 12 gradi ogni giorno rispetto al sole.
Per riassumere il cono della luna ha misure simili a quello del sole, anche se risulta essere appena più basso. La descrizione dovrà poi tenere conto anche di altri fattori quali l’inclinazione variabile nel tempo del cono.
Si tenga poi conto del fatto che il cono è una semplificazione geometrica che non tiene conto delle variazioni in altezza del percorso della luna che generano l’analemma lunare, fenomeno del tutto analogo all’anelemma solare e di cui discuteremo in seguito.
Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Tra le sue migliori scoperte c’è la reintroduzione dell’etere nella fisica della terra piatta e una nuova visione della natura della luce.
E’ coautore del libro “The real measures of the (flat) Earth” edito da Aracne editore e del blog “rifugiatidipella.com“. Dal 2019 produce materiale video inerente la Terra piatta sul suo canale Youtube “earthmeasured”.