di Michele Vassallo su Altrogiornale
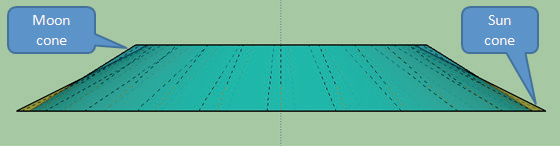
Quando si considera la Terra ferma e piatta, il sole deve necessariamente muoversi su una traiettoria conica. Allo stesso modo la luna, nel suo movimento nel firmamento, deve seguire una traiettoria che si sviluppa su una forma di cono. Si legga anche l’articolo “Il cono del sole sulla Terra piatta“.
Quando consideriamo gli angoli di elevazione della luna quando essa si trovi sui tropici, possiamo provare lo stesso calcolo trigonometrico che abbiamo fatto per il sole. A prima vista si può determinare che il movimento della luna pare un po’ più complicato di quello del sole. Ad esempio, la velocità periferica è minore di quella del sole. Essa perde, rispetto al luminare maggiore, 12° o 48 minuti ogni giorno.
Se avete la possibilità di usare un software di simulazione del moto dei due luminari, potete estrarre alcuni dati che mostreranno che la traiettoria lunare si sviluppa, proprio come il sole, su di un cono, o più precisamente è una spirale che giace su un cono.
Feci queste analisi nel 2017 utilizzando un software e posizionando il punto di osservazione a Roma. Riporto dunque alcuni dati relativi a quell’anno. Il 22 febbraio 2017 la luna toccò il punto più basso del mese. L’angolo di elevazione era di 29.2°. D’altra parte, il 6 marzo 2017, meno di 14 giorni dopo, la luna stava salendo per arrivare ad un angolo di 67,4° che era l’elevazione massima per quel mese. Ciò è stato possibile perché, il 22 febbraio, essa era sull’orbita più bassa del cono (vicino al tropico del Capricorno) mentre, il 6 marzo, era sull’orbita superiore (vicino al tropico del Cancro).
Riporto di seguito una tabella con l’altezza massima e minima della luna durante l’anno 2017. Questo significa che sono andato a ricercare i punti in cui essa era agli estremi della sua traiettoria. Si può vedere dalla tabella che nell’arco di pochi giorni la luna passa dal punto più basso al punto più alto della traiettoria.
| Data | Elevazione minima | Elevazione massima |
| 21 mar 2017 | 29° | |
| 3 apr 2017 | 67,4° | |
| 18 apr 2017 | 29° | |
| 1 mag 2017 | 67,7° | |
| 15 mag 2017 | 28,5° | |
| 28 mag 2017 | 67,6° | |
| 11 giu 2017 | 28,5° | |
| 24 giu 2017 | 68° | |
| 8 lug 2017 | 28,6° | |
| 21 lug 2017 | 67,8° | |
| 4 ago 2017 | 28,5° | |
| 18 ago 2017 | 67,9° | |
| 1 sett 2017 | 28,5° | |
| 14 sett 2017 | 67.8° | |
| 28 sett 2017 | 28,4° | |
| 11 ott 2017 | 67,8° | |
| 25 ott 2017 | 28,2° | |
| 8 nov 2017 | 68,4° | |
| 22 nov 2017 | 28,1° | |
| 6 dic 2017 | 68,3° | |
| 19 dic 2017 | 27,8° |
Come si può notare, la luna viaggia su un cono che ha l’orbita più bassa a circa 28°, considerando la latitudine di Roma, e l’orbita superiore a circa 68°.
Possiamo concludere che, esattamente come il sole, il luminare minore si trova su un cono e questo cono viene percorso, su e giù, in 27, 32 giorni, che è il periodo siderale della luna. Si può verificare questo numero contando quanto ci impiega la luna da un punto di massimo a tornare al punto di massimo successivo. Questo è il periodo che la luna impiega per raggiungere due volte la stessa stella nell’emisfero celeste. Quindi, nel momento in cui il sole fa un ciclo sul suo cono in 365,25 giorni, la luna ripete la sua traiettoria conica per più di 13 volte.
Il cono della luna, anche se molto simile a quello del sole, non è esattamente lo stesso. Probabilmente ricorderete il fatto che gli angoli di elevazione del sole a Roma nei solstizi sono 71,5° e 24,7°. Questi sono valori leggermente diversi dai valori medi del cono di luna misurati per il 2017. La pendenza dei due coni è diversa: gli astronomi affermano che esiste un angolo di 5° di differenza tra l’eclittica (la traiettoria del sole) e la traiettoria della luna.
Curioso è il fatto che questa inclinazione cambi nel corso degli anni. Aggiungo ora una tabella per l’anno 2004 per chiarire questo aspetto.
| Data | Elevazione minima | Elevazione massima |
| 6 gen 2004 | 75,6° | |
| 20 gen 2004 | 20,7° | |
| 2 feb 2004 | 75,7 | |
| 16 feb 2004 | 20,6° | |
| 29 feb 2004 | 75,6° | |
| 15 mar 2004 | 20,5° | |
| 28 mar 2004 | 76,1° | |
| 11 apr 2004 | 20,2° | |
| 25 apr 2004 | 76,1° | |
| 8 mag 2004 | 20,2° | |
| 21 mag 2004 | 75,6° | |
| 5 giu 2004 | 20,3° | |
| 18 giu 2004 | 76,1° | |
| 2 lug 2004 | 20,3° | |
| 26 lug 2004 | 75,9° | |
| 29 lug 2004 | 20,3° | |
| 12 ago 2004 | 76,2° | |
| 25 ago 2004 | 20° | |
| 8 sett 2004 | 76,5° | |
| 22 sett 2004 | 20,2° | |
| 6 ott 2004 | 76,5° | |
| 19 ott 2004 | 19,8° | |
| 2 nov 2004 | 76,7° | |
| 15 nov 2004 | 19,8° | |
| 29 nov 2004 | 76,5° | |
| 12 dic 2004 | 20,1° | |
| 27 dic 2004 | 76,4° |
Come possiamo dedurre, gli angoli della luna nel 2004 sono diversi da quelli del 2017. Sembra che il cono della luna cambi angolo attorno al cono del sole. Questo accade con un ciclo di 18,75 anni di cui abbiamo già parlato nell’articolo “La precessione degli equinozi sulla Terra piatta “. Nell’immagine seguente ho provato a disegnare al CAD il cono della luna, per l’anno 2004, assieme al cono del sole, in modo da sottolineare la differenza di inclinazione.
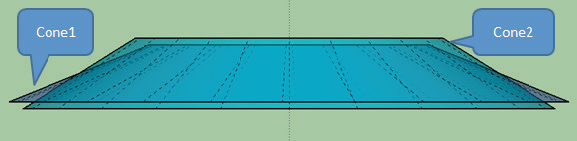
In questa seconda immagine, ho disegnato entrambi i coni della luna, quello del 2004 e quello del 2017 uno sopra l’altro. Si può osservare di quanto sia cambiata l’inclinazione.
I punti in cui l’orbita della luna va a tagliare l’eclittica si chiamano nodi lunari. Il nodo ascendente Ω è il punto di intersezione in salita; il nodo discendente ɣ è quello per il quale si passa in fase di discesa. La linea che congiunge i due nodi è detta “congiungente” i due nodi. La luna dunque oscilla nelle sue rivoluzioni siderali da -5 a +5 gradi rispetto all’eclittica in un arco di tempo di 18,75 anni.
Sulla Terra piatta questa intersezione può essere visualizzata dall’intersezione dei due coni dei due luminari. I due nodi non sono fissi ma si spostano continuamente sull’orbita in senso retrogrado e compiono un giro completo rispetto alle stelle in 6793,39 giorni pari a 18,75 anni. Questo fenomeno è detto retrogradazione dei nodi. E’ analogo alla precessione degli equinozi, e viene chiamato nutazione. Questo produce una variazione dell’angolo di elevazione massimo della luna. Descrive cioè questo cambio di inclinazione del cono nell’arco di alcuni anni.
Il numero di 6793,39 non può di certo passare inosservato. Quando abbiamo discusso in passato della precessione degli equinozi (un ritardo che il sole subisce rispetto alle stelle) dicemmo infatti che essa è data, nella nostra descrizione frattale, da un ciclo completo di 26640 anni che significa un grado ogni 74 anni. Dicemmo poi che 26640/1440=18.5 esprimendo con 18,5 anni un ciclo completo di retrogradazione dei nodi lunari. Andiamo ora a fare qualche calcolo:
6793.39=6660+120+12+1.2+0.12+…=6660+6660/55.5+6660/555+6660/5550+6660/55500+…
Vediamo, quindi come nella descrizione frattale cui ormai siamo abituati, un ciclo di retrogradazione dei nodi o nutazione non sia altro che un’intersezione tra 666 e 555 e il corpo principale sia descrivibile dal nostro 6660. 6660 giorni diviso 360 ci da 18,5 anni. Un ciclo di retrogradazione dei nodi quindi ci sta 1440 volte in un ciclo di precessione. Esattamente come un minuto ci sta 1440 volte in 24 ore. La nutazione dunque è il minuto nella giornata data dal ciclo di precessione.
Provo a fare un riepilogo.
Il sole ha una traiettoria che copre un cono completo, su e giù, in un anno o 365,25… giorni. La luna percorre una traiettoria adagiata su un cono simile, ma va su e giù in 27,32 giorni.
Il cono della luna è leggermente inclinato rispetto a quello del sole, con un angolo di circa più o meno 5°.
Questo angolo cambia anno dopo anno da (circa) meno cinque a più cinque in 18,5 anni. Questo movimento si chiama librazione della luna in latitudine o anche nutazione lunare.
Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Tra le sue migliori scoperte c’è la reintroduzione dell’etere nella fisica della terra piatta e una nuova visione della natura della luce.
E’ coautore del libro “The real measures of the (flat) Earth” edito da Aracne editore e del blog “rifugiatidipella.com“. Dal 2019 produce materiale video inerente la Terra piatta sul suo canale Youtube “earthmeasured”.