di Michele Vassallo da Altrogiornale
Questo articolo va a demolire uno dei pilastri fondamentali della Terra globulare: la formula della gravitazione universale di Newton. Se questa formula fosse valida la Terra dovrebbe essere necessariamente un globo. La scienza dice infatti che, a causa della forza di gravità, tutti i corpi celesti sopra i 500 km di diametro devono necessariamente essere sferici. Facciamo dunque un passo grande quanto necessario per progredire nella verità.
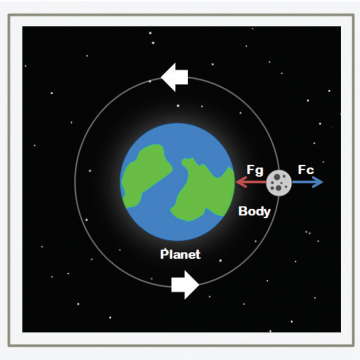
Un corpo in orbita intorno ad un pianeta è in equilibrio tra due forze: la forza centrifuga e quella gravitazionale.
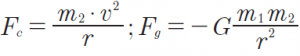
dove Fc è la forza centrifuga, Fg è la forza gravitazionale, m2 è la massa del corpo in orbita, m1 è la massa del pianeta, v è la velocità del corpo durante l’orbita, r è la distanza del corpo da il centro del pianeta, G è la costante gravitazionale:
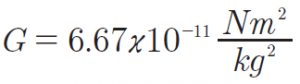
Il segno è negativo perché la forza è di attrazione. Il corpo orbitante è caratterizzato da una energia potenziale chiamata “gravitazionale” causata dal campo in cui è immersa. Quando si parla di energia potenziale, la mente corre immediatamente al teorema di Bernoulli, che afferma che, per un liquido, la somma di energia potenziale, cinetica e di pressione è costante. Si potrebbe pensare all’acqua contenuta in un bacino che si trova sulla cima di una montagna, acqua che è costretta a passare in una condotta, trasformando, a causa dell’altitudine, il potenziale iniziale in energia cinetica e di pressione. Successivamente verrà raccolta in una turbina per trasformare l’energia in elettricità.
Il teorema di Bernoulli è un’applicazione del principio di conservazione dell’energia. L’energia cambia forma ma la sua quantità totale non cambia. Nel caso di una condotta forzata, l’energia potenziale dell’acqua in quota viene trasformata in energia cinetica e in energia di pressione.
U = mgh è la formula per l’energia potenziale mentre Ec = 1/2 mv2 è l’energia cinetica.
Il principio della conservazione dell’energia potrebbe essere, allo stesso modo, applicato a un’orbita del corpo nel campo gravitazionale di un pianeta. In un campo gravitazionale, l’energia potenziale è espressa dalla formula generale:
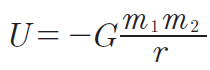
L’espressione U = m ∙ g ∙ h (a cui tutti eravamo abituati a scuola) è un caso particolare della precedente espressione più generale, e può essere applicata solo nel caso di h << R dove R è il raggio della Terra (questo significa che è valida solo a livello del suolo).
Il principio di conservazione dell’energia per un corpo in un campo gravitazionale è espresso dalla relazione:
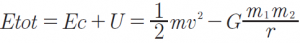
La quantità totale di energia è la somma dell’energia cinetica e potenziale.
Quindi, secondo questa relazione, un corpo in caduta libera nel campo gravitazionale di un pianeta convertirà la sua energia potenziale in energia cinetica, mantenendo costante la somma delle due.
La quantità totale di energia rimarrà la stessa. Per aumentare l’energia potenziale di un corpo fermo, non posso diminuirne ulteriormente la velocità. Dovrò aggiungere dell’energia esterna al sistema.
Così, in una centrale idroelettrica, l’acqua viene guidata per tutta la notte fino al lago a monte, consumando energia elettrica che, durante la notte, ha un costo inferiore. Tuttavia è evidente la necessità di spendere dell’energia al fine di portare l’acqua in alto ottenendo così un lago di nuovo pieno da poter sfruttare durante il giorno quando si può vendere l’energia ad un prezzo maggiore. Un altro esempio potrebbe essere relativo a uno scivolo su cui è possibile scivolare verso il basso senza alcuno sforzo ma, quando si sale nella direzione opposta, è necessario aggiungere una buona quantità di energia nel rispetto della legge di conservazione.
Immaginiamo una situazione simile considerando un corpo in orbita che si muove solo in direzione orbitale e non in direzione radiale. Il corpo, quindi, possiede solo energia potenziale. Non ha energia di movimento nella direzione di allontanamento dal pianeta, in quanto si mantiene sempre alla stessa quota.
Consideriamo ora un meteorite a cui capita di colpire il satellite in direzione tangenziale all’orbita andando in questo modo ad aumentarne, appena di un po’, la velocità: un aumento molto piccolo.
La nuova velocità acquisita dal satellite considerato è v ‘= v + Δv, dove Δv è molto piccolo. Tuttavia, poiché v’ è maggiore di v seppur di poco, la forza centrifuga cresce leggermente, secondo la relazione:

La forza gravitazionale, d’altra parte, rimane la stessa perché non è influenzata dalla velocità. L’equilibrio viene quindi perso e sul satellite agisce quindi una forza
F risultante = Fc’- Fg
sufficiente a trascinarlo via dal pianeta. La forza risultante genera una accelerazione nella direzione radiale. L’energia cinetica, muovendosi il satellite in direzione radiale, da zero inizia ad aumentare e il satellite si allontana dal pianeta. Poiché la distanza cresce (r cresce), Fc’ diminuisce in proporzione a 1 / r. Nello stesso tempo la forza di gravità (la famosa formula della gravitazione di Newton):
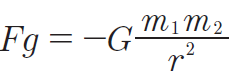
diminuisce più velocemente, in proporzione a 1 / r2. Il corpo accelera dunque sempre di più e l’energia cinetica cresce a questo punto molto velocemente. Questo avviene senza aggiunta di energia esterna, a parte la piccolissima energia iniziale dell’urto. Allo stesso tempo, dato che il corpo si sta allontanando dal pianeta, l’energia potenziale cresce, esattamente come l’energia cinetica. L’energia totale dunque cresce con il contributo di entrambi i termini cinetico e potenziale, senza aver ricevuto un reale contributo esterno di energia.
E qui capiamo il paradosso. Il corpo dovrebbe immediatamente fermarsi attorno al pianeta intrappolato in un’altra orbita, perché, aumentando la distanza, aumenta l’energia potenziale e quindi dovrebbe diminuire l’energia cinetica di una quantità pari all’energia impressa dall’urto del meteorite. Questo direbbe il principio di conservazione dell’energia. Invece, in conseguenza del fatto che la forza centrifuga continuerà ad essere maggiore della forza gravitazionale, il corpo continuerà ad allontanarsi dal pianeta. Questo significa creazione di energia dal nulla. Al diavolo il principio della conservazione dell’energia!
Un’obiezione che potrebbe essermi fatta è che l’energia potenziale non cresce ma diminuisce quando il satellite si allontana dal pianeta. In realtà l’energia potenziale viene convenzionalmente fissata a zero ad una distanza infinita dal pianeta stesso ed è sempre negativa, crescente verso l’infinito.Bisogna quindi essere attenti quando si considera il segno dell’energia che è sempre negativo. È un’energia negativa che cresce con l’allontanamento dal pianeta fino a zero.
Calcoliamo, solo per fare un esempio pratico, l’energia totale di un razzo di 10000 kg che si muove alla velocità di 500 m/sec e che si sta allontanando dal pianeta. Eseguiremo il calcolo considerando prima un raggio r1 = 500 km e poi r2 = 1000 km per vedere come varia l’energia potenziale. Non c’è propulsione: il razzo si sta allontanando dalla Terra a causa di una spinta precedente e, poiché si muove nel vuoto, nulla sta rallentando il suo moto o riducendo la sua velocità:
La sua energia cinetica è: Ec=1/2mV2=1.25E9 Joule
L’energia potenziale, considerando che la massa della Terra è M = 5,97 E24 kg è:
a 500 km:U=-Gm1m2/r=-7.96E12 Joule
a 1000 km: U=-Gm1m2/r=-3.98 E12 Joule
7,96 sembra essere maggiore di 3,98 ma non lo è perché son valori negativi.
L’energia totale sarà dunque a 500 km: Etot=Ec+U=-7.958 E12 Joule
E a 1000 km: Etot=Ec+U=-3.978 E12 Joule
Questo secondo valore è molto più grande. E’ evidente dunque che la quantità di energia totale non si conserva. La formula gravitazionale di Newton non rispetta il principio di conservazione dell’energia: la gravità di Newton è un grande inganno.
Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Tra le sue migliori scoperte c’è la reintroduzione dell’etere nella fisica della terra piatta e una nuova visione della natura della luce.
E’ coautore del libro “The real measures of the (flat) Earth” edito da Aracne editore e del blog “rifugiatidipella.com“. Dal 2019 produce materiale video inerente la Terra piatta sul suo canale Youtube “earthmeasured”.